Lagrangian Coherent Structures

(and the finite-time Lyapunov exponent)

If video breaks:

https://www.youtube.com/watch?v=CCmTY0PKGDs

A Lagrangian coherent structure (LCS) is a region in a fluid that remains “coherent” under the flow.

LCSs are a generalisation of easily identifiable structures such as jets and vortices.

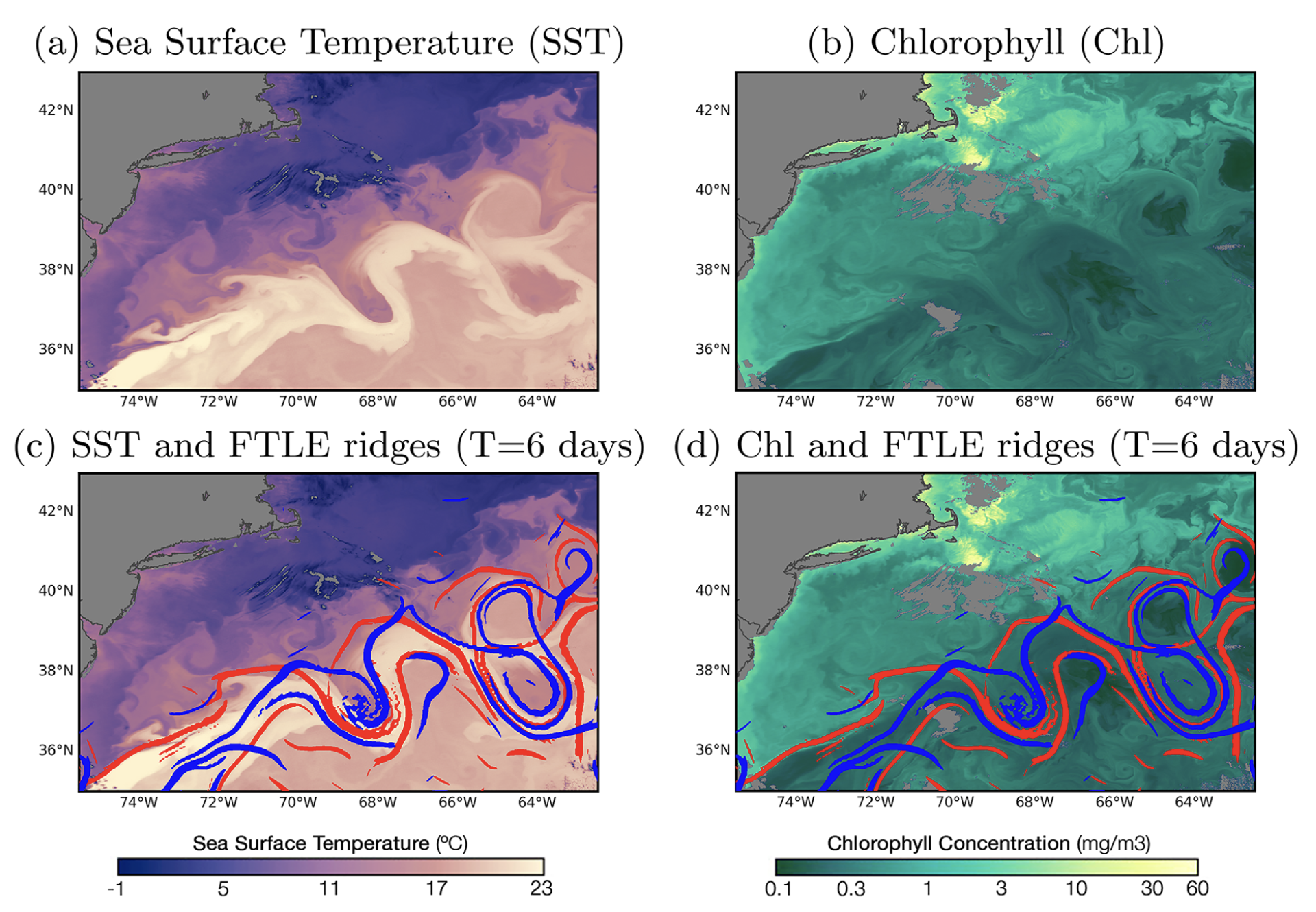
Y. Liu, C. Wilson, M.A. Green, C.W. Hughes, 2018. Gulf Stream Transport and Mixing Processes via Coherent Structure Dynamics. Journal of Geophysical Research: Oceans 123, 3014–3037.

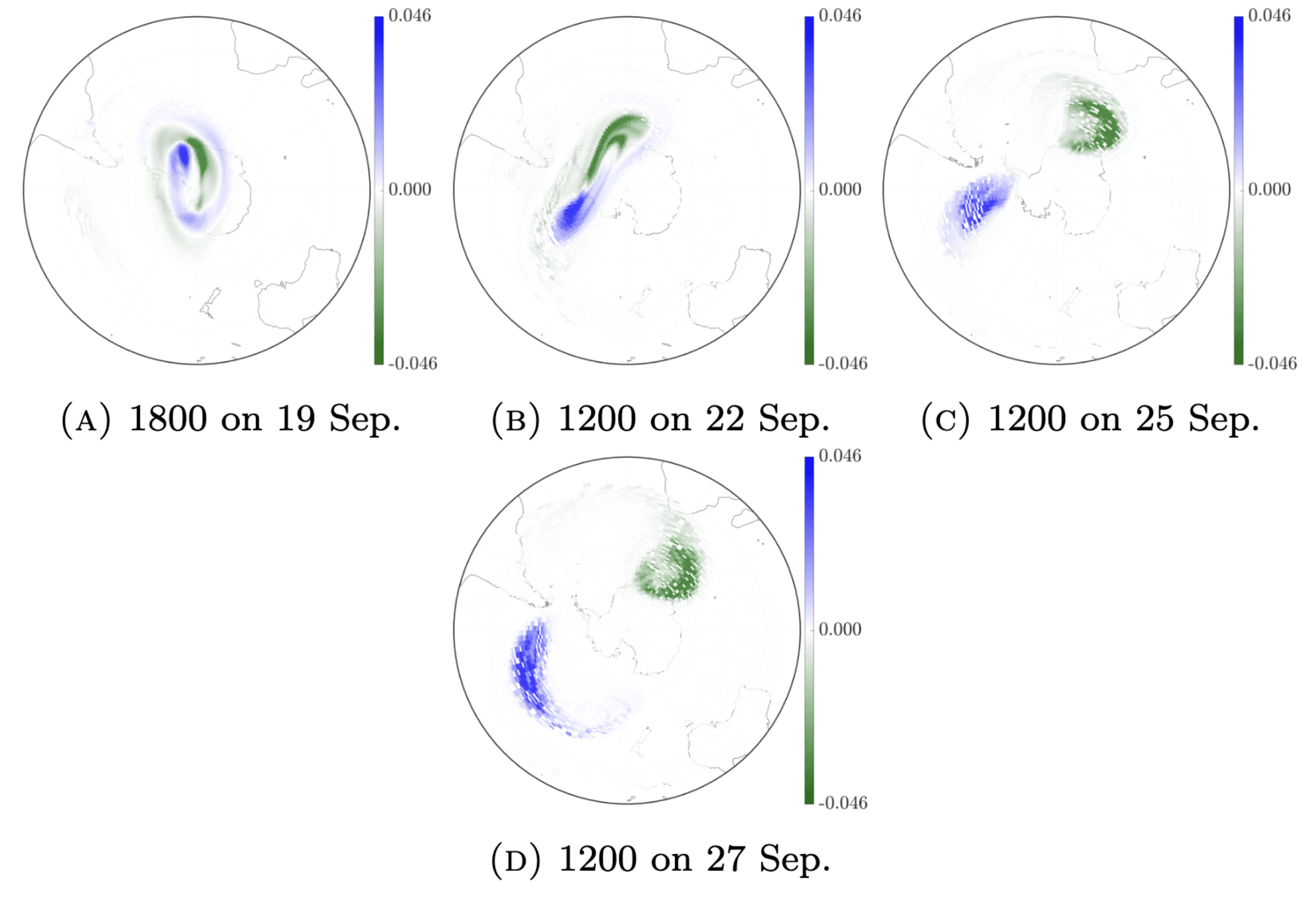
C. Blachut and C. González-Tokman, 2020. A tale of two vortices: How numerical ergodic theory and transfer operators reveal fundamental changes to coherent structures in non-autonomous dynamical systems. Journal of Computational Dynamics 7, 369–399.

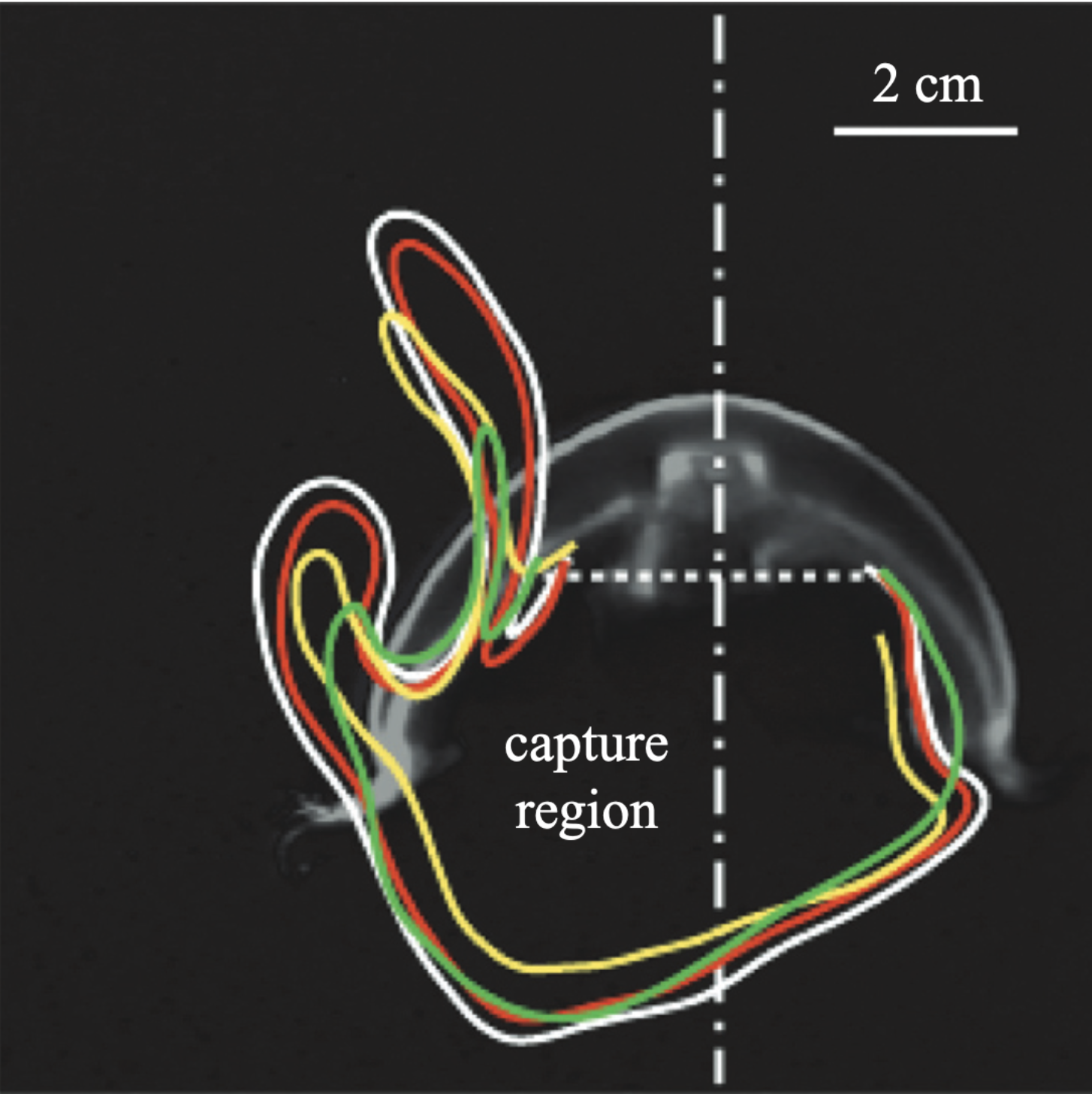
J. Peng and J.O. Dabiri, 2009. Transport of inertial particles by Lagrangian coherent structures: application to predator–prey interaction in jellyfish feeding. Journal of Fluid Mechanics 623, 75–84.

The velocity at a point \(x \in \Omega_0\) and time \(t \in [0,T]\) is given by the Eulerian velocity \[ u(x,t) \]

The Lagrangian trajectories \(X(t)\) solve \[ \frac{\mathrm{d}X}{\mathrm{d}t} = u\left(X, t\right), \quad X(0) = x \]

Define the flow map \(F_0^t(x)\) as

\[ \frac{\partial F_0^t(x)}{\partial t} = u\left(F_0^t(x), t\right), \quad F_0^0(x) = x \]

LCSs are often computed only from the flow map \(F_0^t(x)\).

An example: the finite-time Lyapunov exponent (FTLE)

The goal: characterise stretching.

\[ \sigma\left(x\right) = \frac{\left|\!\left|F_0^t\left(x + \delta\right) - F_0^t\left(x\right)\right|\!\right|}{\left|\!\left|\delta\right|\!\right|} \]

\[ \sigma\left(x\right) = \frac{\left|\!\left|F_0^t\left(x + \delta\right) - F_0^t\left(\delta\right)\right|\!\right|}{\left|\!\left|\delta\right|\!\right|} \approx \frac{\left|\!\left|\nabla F_0^t\left(x\right)\delta\right|\!\right|}{\left|\!\left|\delta\right|\!\right|} \]

\[ \mathrm{FTLE}\left(x,t\right) = \frac{1}{t}\ln\left[\max_{\delta \neq 0}\frac{\left|\!\left|\nabla F_0^t(x)\delta\right|\!\right|}{\left|\!\left|\delta\right|\!\right|}\right]. \]

How to extract LCSs from the FTLE field?

Maximising ridges can correspond to attracting/repelling regions.
Such regions form barriers and jets in the flow.

S.C. Shadden, F. Lekien, J.E. Marsden, 2005. Definition and properties of Lagrangian coherent structures from finite-time Lyapunov exponents in two-dimensional aperiodic flows. Physica D: Nonlinear Phenomena 212, 271–304.

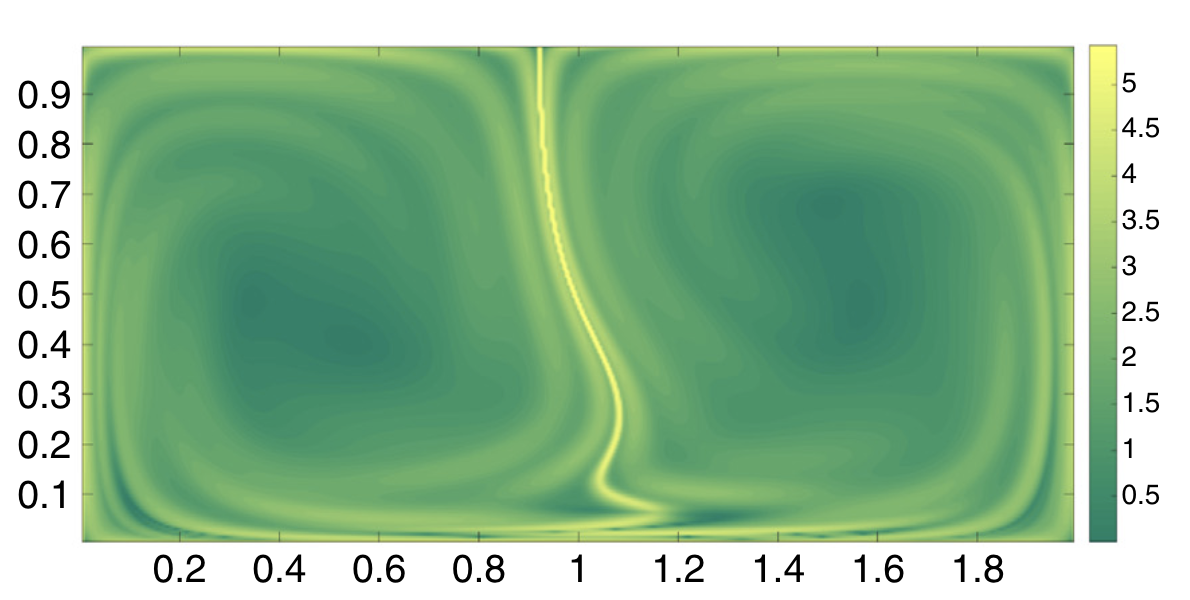
S. Balasuriya, N.T. Ouellette, I.I. Rypina, 2018. Generalized Lagrangian coherent structures. Physica D: Nonlinear Phenomena 372, 31–51.